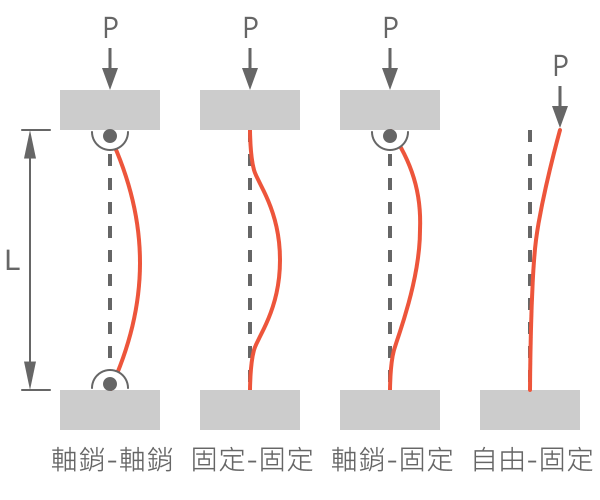
油壓缸強度計算
當長行程的油壓缸應用在推力場合時,由於是細長的結構件,我們必須考慮挫屈強度,避免軸桿產生不穩定的彎曲。 輸入油壓缸的尺寸,快速計算各種安裝方式的允許最大推力,以及當下的供油壓力。
固定方式
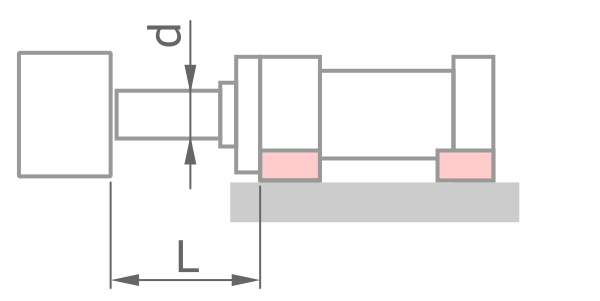
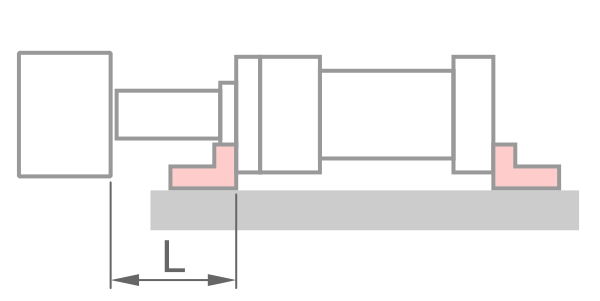


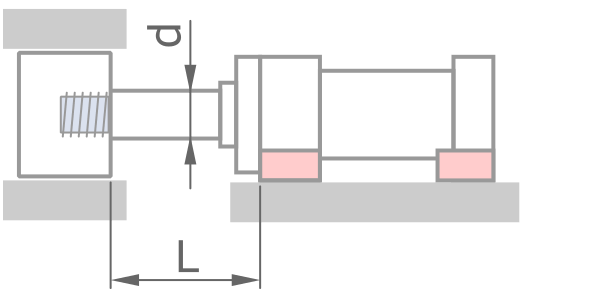
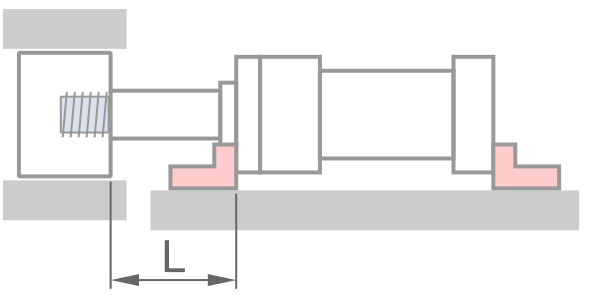
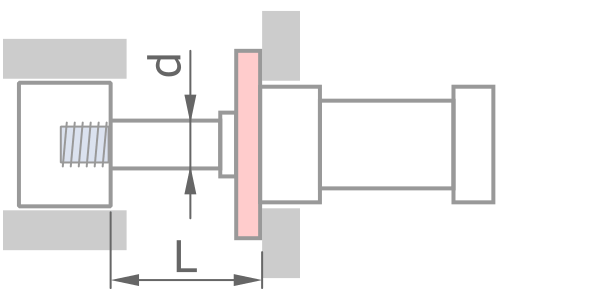

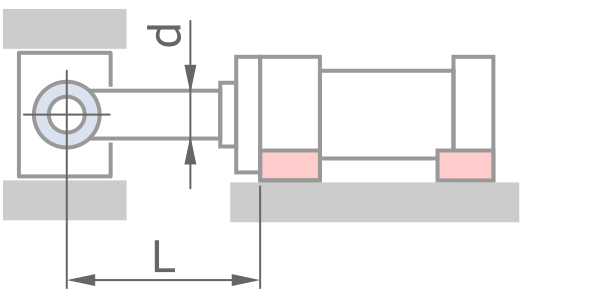
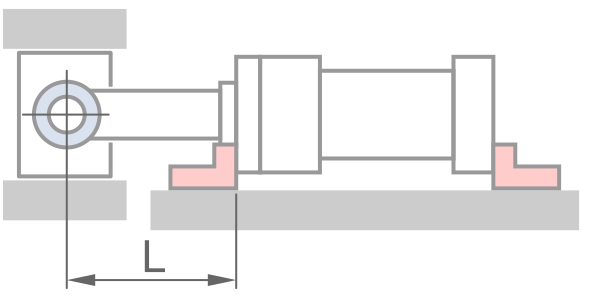
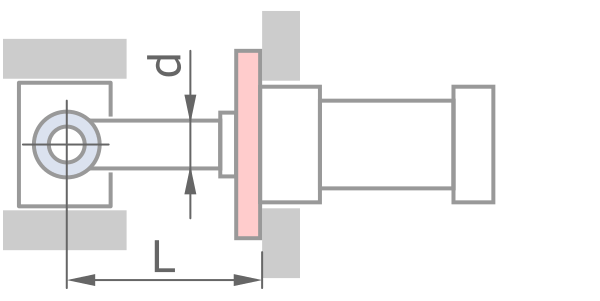
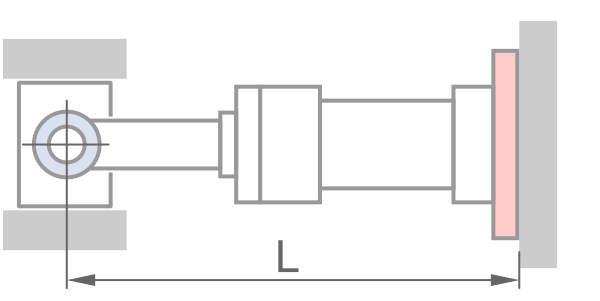

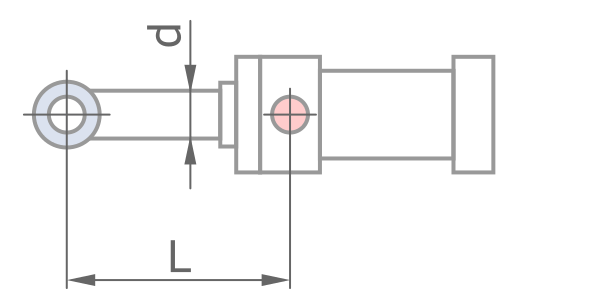
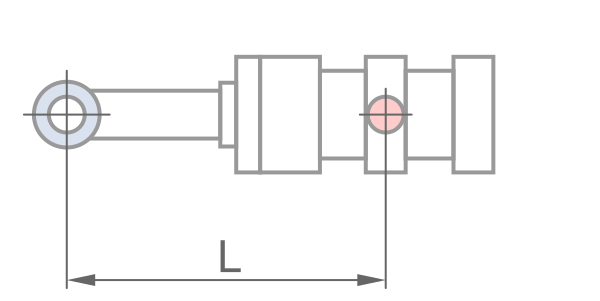
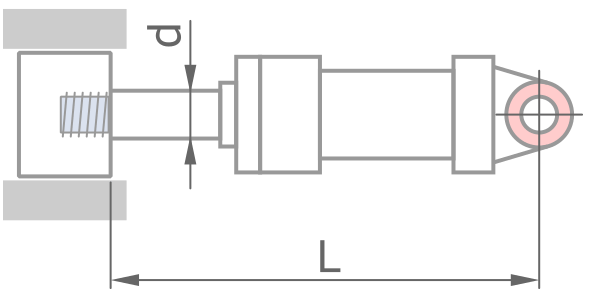

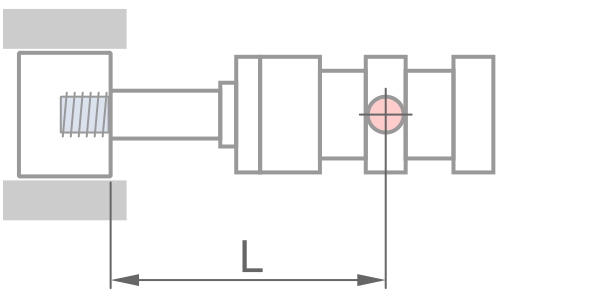
鋼材性質 - 預設值適用一般情況
安全係數
允許最大推力
允許最高油壓
細長比
slenderness ratio
軸桿壓應力
允許最大推力
細長柱體的挫屈臨界負載自 1757 年 Euler 提出後,一直廣泛應用於細長構件的強度設計。 然而短柱體在還沒挫屈之前,就先產生了永久變形,無法使用 Euler 方程來預測,這時我們需要借助其他的方程,如 Johnson 與 Tetmajer (本計算器) 分別使用拋物線、直線來預測短柱體的臨界負載。 臨界負載在考量安全係數後,即是結構件所能允許的最大受力。
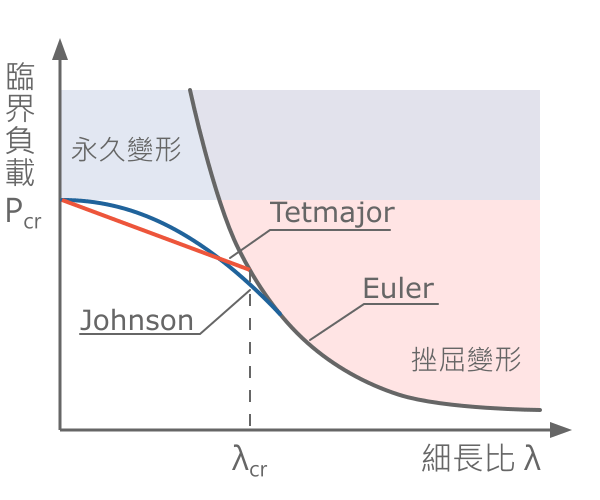
\[
\text{Euler - Tetmajer 方程:} \\[24pt]
當 \; \lambda > \lambda_{cr} , \quad \lambda = {4L_e \over d} , \quad \lambda_{cr} = \pi \sqrt{E \over {0.8S_y}} \\[12pt]
\quad P_{cr} = {\pi^2 EI \over {nL_e^2}} \\[24pt]
當 \; \lambda \leq \lambda_{cr} \\[12pt]
\quad P_{cr} = {d^2 \pi (S_y - 0.62 \lambda) \over {4 n}} \\[24pt]
\]
\[
式中 \\[6pt]
\begin{align*}
\quad &n: & &安全係數 \\
\quad &d: & &軸徑 & \, &\{ m \} \\
\quad &E: & &彈性係數 & \, &\{ Pa \} \\
\quad &S_y: & &降伏強度 & \, &\{ Pa \} \\
\quad &I: & &斷面慣性矩 & \, &\{ m^4 \} = {{\pi d^4} \over 64} \\
\quad &L_e: & &等效長度 & \, &\{ m \} \\
\end{align*}
\]
\[
\\[24pt]
\quad =
\begin{cases}
2L, &固定 - 自由 \\
L, &軸銷 - 軸銷 \\
0.7L, &固定 - 軸銷 \\
0.5L, &固定 - 固定 \\
\end{cases}
\]